Technique
opératoire
Un matériel stabilisé
pour une hanche dynamique
Calcul
de la position mathématique idéale de
la vis
à l'intérieur de la tête fémorale |
SURFACE DU SEGMENT DE SPHERE EN FONCTION
DE h (calotte sphérique)
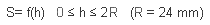
| h (mm) |
Surface Sphérique
S1 (cm2) |
Surface de la base
S2 (cm2) |
Surface Totale
S3 = S1+ S2 (cm2) |
| 0 |
0 |
0 |
0 |
| 4 |
6,03188 |
5,52903 |
11,56106 |
| 8 |
12,06372 |
10,05310 |
22,11681 |
| 12 |
18,09557 |
13,57168 |
31,66725 |
| 13 |
19,60354 |
14,29425 |
33,89779 |
| 16 |
24,12743 |
16,08495 |
40,21239 |
| 20 |
30,15929 |
17,59292 |
47,75221 |
| 24 |
36,19115 |
18,09557 |
54,28672 |
| 27 |
40,715042 |
17,81283 |
58,52787 |
| 28 |
42,22301 |
17,59292 |
59,81592 |
| 32 |
48,25486 |
16,08495 |
64,33982 |
| 36 |
54,28672 |
13,57168 |
67,85840 |
| 40 |
60,31858 |
10,05310 |
70,37168 |
| 44 |
66,35044 |
5,52920 |
71,87964 |
| 48 |
72,38230 |
0 |
72,38230 |
 Dans
ce tableau, on constate que plus la hauteur de la calotte
est grande, plus la surface sphérique est élevée.
Ainsi, pour h = 8 mm, on obtient une surface de 12 cm2
au-dessus de la broche. Ceci ne tient pas compte de l'extrémité
de la vis céphalique que l'on fixe dans la tête.
Les spires de cette vis ont en effet - en moyenne - un rayon
d'environ 5 mm. Il ne reste donc plus en réalité
au-dessus de la vis qu'une calotte sphérique de 3 mm
de hauteur. Ceci ne laisse plus qu'une surface d'environ 5
cm2. Il en est de même, pour les mêmes
raisons, pour les calottes sphériques dont les hauteurs
sont les plus élevées. On ne doit donc pas utiliser
les zones extrêmes, celles situées au dessous
de 12 mm - situées près de la zone portante
- et celles au dessus de 36 mm - situées au pôle
inférieur - pour une tête fémorale de
48 mm de diamètre. Dans
ce tableau, on constate que plus la hauteur de la calotte
est grande, plus la surface sphérique est élevée.
Ainsi, pour h = 8 mm, on obtient une surface de 12 cm2
au-dessus de la broche. Ceci ne tient pas compte de l'extrémité
de la vis céphalique que l'on fixe dans la tête.
Les spires de cette vis ont en effet - en moyenne - un rayon
d'environ 5 mm. Il ne reste donc plus en réalité
au-dessus de la vis qu'une calotte sphérique de 3 mm
de hauteur. Ceci ne laisse plus qu'une surface d'environ 5
cm2. Il en est de même, pour les mêmes
raisons, pour les calottes sphériques dont les hauteurs
sont les plus élevées. On ne doit donc pas utiliser
les zones extrêmes, celles situées au dessous
de 12 mm - situées près de la zone portante
- et celles au dessus de 36 mm - situées au pôle
inférieur - pour une tête fémorale de
48 mm de diamètre.

ANALYSE de la COURBE des SURFACES
 Pour
les mêmes raisons que pour les volumes, les deux extrémités
de la droite des surfaces sphériques ne peuvent être
utilisées comme zone de positionnement de la broche.
Lorsque la hauteur "h" des zones A et A' sont comprises
entre zéro et treize millimètres, la surface
de base (S2) est nulle. Elle ne peut donc accepter une vis-plaque.
C'est la zone interdite. Pour
les mêmes raisons que pour les volumes, les deux extrémités
de la droite des surfaces sphériques ne peuvent être
utilisées comme zone de positionnement de la broche.
Lorsque la hauteur "h" des zones A et A' sont comprises
entre zéro et treize millimètres, la surface
de base (S2) est nulle. Elle ne peut donc accepter une vis-plaque.
C'est la zone interdite.
 Si
la zone B comprise entre treize et vingt-quatre millimètres
(pour une sphère de quarante-huit millimètres)
a une bonne surface de base (S2), la surface de la calotte
sphérique (S1), dans la moitié supérieure
de la tête au contact du toit du cotyle, est faible
- moins de la moitié de cette surface. Si la surface
totale (S3) augmente très rapidement pour de faibles
valeurs de "h", on ne peut envisager de mettre en
place une broche au-dessous d'une valeur d'au moins la moitié
de cette surface. Si les spires de la vis sont incluses dans
cette zone, elles seront recouvertes d'une épaisseur
suffisante pour éviter les balayages - à condition
que la tête fémorale ne soit pas ostéoporotique.
C'est la zone de tolérance. Si
la zone B comprise entre treize et vingt-quatre millimètres
(pour une sphère de quarante-huit millimètres)
a une bonne surface de base (S2), la surface de la calotte
sphérique (S1), dans la moitié supérieure
de la tête au contact du toit du cotyle, est faible
- moins de la moitié de cette surface. Si la surface
totale (S3) augmente très rapidement pour de faibles
valeurs de "h", on ne peut envisager de mettre en
place une broche au-dessous d'une valeur d'au moins la moitié
de cette surface. Si les spires de la vis sont incluses dans
cette zone, elles seront recouvertes d'une épaisseur
suffisante pour éviter les balayages - à condition
que la tête fémorale ne soit pas ostéoporotique.
C'est la zone de tolérance.
 La
largeur maximum est située de part et d'autre de l'équateur
: zone (C). La position idéale est, là encore
dans le quadrant inférieur de la sphère.comprise
entre vingt-quatre et trente millimètres. C'est la
zone idéale. La
largeur maximum est située de part et d'autre de l'équateur
: zone (C). La position idéale est, là encore
dans le quadrant inférieur de la sphère.comprise
entre vingt-quatre et trente millimètres. C'est la
zone idéale.

VOLUME DU SEGMENT DE SPHERE EN FONCTION
DE h (calotte sphérique)
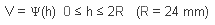
| h (mm) |
Volume V du segment de sphère (cm3) |
Formules utilisées |
| 0 |
0 |
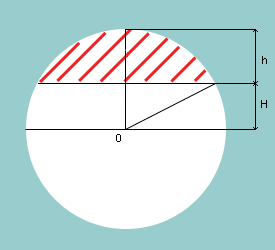
1. V = 1/6  h (3 r2 + h2) avec r2
= (2R - h)
h (3 r2 + h2) avec r2
= (2R - h)
2. V = 1/3  h2 (3R - h)
h2 (3R - h) |
| 4 |
1,13935 |
| 8 |
4,28932 |
| 12 |
9,04779 |
| 13 |
10,44161 |
| 16 |
15,01262 |
| 20 |
21,78171 |
| 21 |
23,55252 |
| 24 |
28,95292 |
| 27 |
34,35332 |
| 28 |
36,12413 |
| 32 |
42,89321 |
| 36 |
48,85805 |
Moyen de contrôle des formules :
- Prendre h = R pour 1 et 2
On doit trouver le volume de la demi-sphère :
v = 2/3  R3
R3 |
| 40 |
53,61652 |
| 44 |
56,76649 |
| 48 |
57,90584 |
NOTA : On constate que si l'on place la broche
dans une calotte où h est de 12 mm, compte tenu du
rayon de la vis fixée dans la tête fémorale
( en moyenne 8 mm), on obtient un volume d'os autour de 3
cm3.

ANALYSE de la COURBE des VOLUMES
 On
constate aux deux extrêmes de la courbe, une augmentation
quasi nulle du volume du segment sphérique. Lorsque
la hauteur est comprise entre zéro et dix millimètres
le volume au dessus de la vis céphalique, est compris
entre zéro et cinq cm3. La zone A est donc
interdite (zone au contact du toit de la cavité cotyloïde). On
constate aux deux extrêmes de la courbe, une augmentation
quasi nulle du volume du segment sphérique. Lorsque
la hauteur est comprise entre zéro et dix millimètres
le volume au dessus de la vis céphalique, est compris
entre zéro et cinq cm3. La zone A est donc
interdite (zone au contact du toit de la cavité cotyloïde).
 Lorsque
l'on est dans la zone A', c'est à dire lorsque h est
compris entre quarante et quarante huit millimètres,
si le volume de la calotte sphérique est à son
maximum au-dessus de la broche, la surface autour de celle-ci
est nulle. On se trouve au pôle inférieur de
la tête fémorale, proche de la cavité
articulaire. Cette zone est donc également interdite. Lorsque
l'on est dans la zone A', c'est à dire lorsque h est
compris entre quarante et quarante huit millimètres,
si le volume de la calotte sphérique est à son
maximum au-dessus de la broche, la surface autour de celle-ci
est nulle. On se trouve au pôle inférieur de
la tête fémorale, proche de la cavité
articulaire. Cette zone est donc également interdite.
 Entre
ces deux extrêmes, l'augmentation de volume de fait
de façon linéaire et progressivement croissante
dans la zone B. Si la broche est placée à quatre
millimètres au-dessus de l'équateur, le volume
est à peine le tiers du volume osseux total. C'est
la zone limite de tolérance. Entre
ces deux extrêmes, l'augmentation de volume de fait
de façon linéaire et progressivement croissante
dans la zone B. Si la broche est placée à quatre
millimètres au-dessus de l'équateur, le volume
est à peine le tiers du volume osseux total. C'est
la zone limite de tolérance.
 La
position idéale de la broche doit donc se situer dans
la moitié inférieure de la tête fémorale
au dessous de son diamètre : c'est la zone C. Dans
le cas où la tête mesure quarante huit millimètres,
lorsque l'on place la broche dans une zone où la hauteur
est comprise entre vingt-quatre et trente-deux mm (moyenne
: 27 mm) on obtient un volume osseux compris entre trente-six
et quarante-deux cm3 dans lequel la vis est entourée
de plus de la moitié. C'est la zone de positionnement
idéal. La
position idéale de la broche doit donc se situer dans
la moitié inférieure de la tête fémorale
au dessous de son diamètre : c'est la zone C. Dans
le cas où la tête mesure quarante huit millimètres,
lorsque l'on place la broche dans une zone où la hauteur
est comprise entre vingt-quatre et trente-deux mm (moyenne
: 27 mm) on obtient un volume osseux compris entre trente-six
et quarante-deux cm3 dans lequel la vis est entourée
de plus de la moitié. C'est la zone de positionnement
idéal.

CONCLUSION
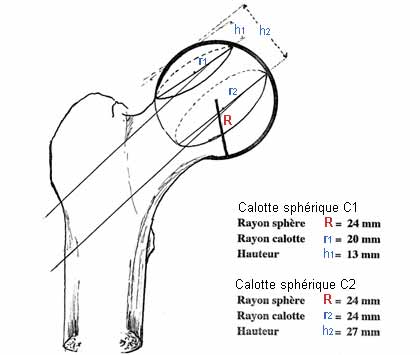
Schéma des calottes sphériques d'une
tête fémorale
 Le
plan des calottes sphériques et le plan matérialisé
par la broche guide ont été volontairement décalés
de quelques degrés pour la clarté du schéma. Le
plan des calottes sphériques et le plan matérialisé
par la broche guide ont été volontairement décalés
de quelques degrés pour la clarté du schéma.
 Les
calculs des calottes sphériques permettent de définir
mathématiquement la zone idéale destinée
à recevoir la broche. Elles sont résumées
dans le schéma final. Les
calculs des calottes sphériques permettent de définir
mathématiquement la zone idéale destinée
à recevoir la broche. Elles sont résumées
dans le schéma final.
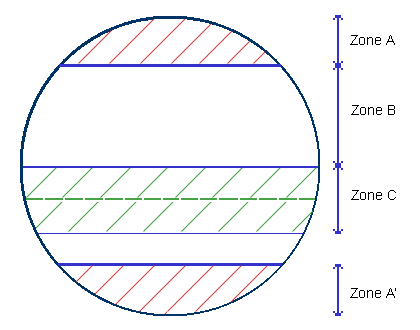
| Schéma : |
Les zones A et A' sont interdites.
La zone B est dite de tolérance, à condition
que les spires
de la vis céphalique ne pénètrent
pas dans la zone interdite.
La zone C est la zone favorable. L'emplacement idéal
se situe
au dessous de l'équateur. Il est matérialisé
par des traits verts. |
Bibliographie :
DENIS-PAPIN M. ; MATHEMATIQUES générales ; DUNOD
Ed. ; 1951 ; 4ème Edition ; IV-V.
HÛTTE ; MANUEL de L'INGENIEUR ; LIBRAIRIE POLYTECHNIQUE
CH. BERANGER Tome I ; 1947 ; 240 – 245.
Remerciements à Mr R .GUYOT, Ingénieur.

:: Fermer la fenêtre :: |


